Material:Vorlesung2.pdf, supp_mat_2.pdf
Basisfunktionen
Nützliche Konzepte
UND, ODER, NICHT Verknüpfung
Schaltnetzanalyse
Zusammengesetzte Gatter
Schaltungen aus Grundgattern
Zusammenfassung
Chapter 3: Boole’sche Algebra
3.2 Schaltvariable und Schaltfunktionen, Signale
In der Schaltalgebra gibt es genau 2 mögliche werte die wir für Variable und Funktionen verwenden 0 und 1. it Schaltfunktionen können Schaltvariable durch spezielle Transformationen, die auch also Gatterfunktionen bezeichnet werden, in einander überführt werden.
3.2 ElementareSchaltfunktionen
Nach definition:
Das Ergebnis einer Schaltfunktion ist 1, wenn durch die Schalteranordnung ein Strom fließen
kann.

Boolean Algebra: The Foundation of Logic Design
Boolean algebra provides the mathematical framework for analyzing and designing digital circuits. It offers a set of rules and axioms for manipulating logical expressions, allowing us to simplify and optimize circuit designs.
Key Axioms and Theorems
The following are some fundamental axioms and theorems of Boolean algebra:
Axioms
- Identity:
- A+0=A
- A⋅1=A
- Complement:
- A+A=1
- A⋅A=0
- Commutativity:
- A+B=B+A
- A⋅B=B⋅A
- Distributivity:
- A⋅(B+C)=(A⋅B)+(A⋅C)
- A+(B⋅C)=(A+B)⋅(A+C)
Duality Principle
A crucial concept is the duality principle. Any valid Boolean equation remains valid if we interchange the AND and OR operations, and replace 1’s with 0’s and vice-versa.
DeMorgan’s Laws
These are fundamental theorems used extensively in logic simplification:
- A+B=A⋅B
- A⋅B=A+B
In essence, applying a NOT gate to the result of an operation (AND or OR) is equivalent to applying NOT gates to each operand and then performing the opposite operation (OR or AND, respectively).
Logic Synthesis and Computer-Aided Design (CAD)
The power of Boolean algebra lies in its ability to simplify complex logic expressions. By applying these rules and theorems, we can reduce the number of gates required to implement a particular function, leading to more efficient circuits in terms of area, power consumption, and delay. This process, called logic minimization or logic simplification, is often automated using Computer-Aided Design (CAD) or Electronic Design Automation (EDA) tools, making it possible to design and optimize complex digital systems with millions or even billions of gates. Because at such scales, hand optimisation is intractable.
Standardized Function Representations (Canonical Forms)
To facilitate communication, analysis, and automated design, it’s crucial to have standardized, universally accepted ways of representing Boolean functions. These are known as canonical representations, which start from a function’s truth table.
There are two primary canonical forms:
- Sum of Products (SOP): Also known as Disjunctive Normal Form (DNF).
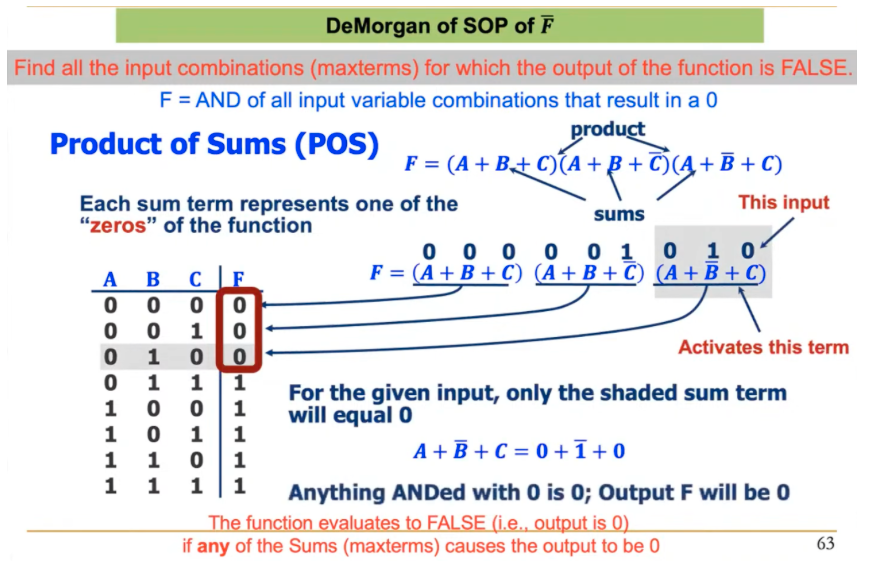
- Product of Sums (POS): Also known as Conjunctive Normal Form (CNF).
Definitions
Before diving into the forms, let’s define some key terms:
- Complement: The complement of a variable is its negation (e.g., the complement of A is A).
- Literal: A variable or its complement (e.g., A, A, B, B).
- Implicant: A product term (AND term) that implies the function (i.e., if the product term is 1, then the function is 1). It can be a single literal or a combination of literals ANDed together.
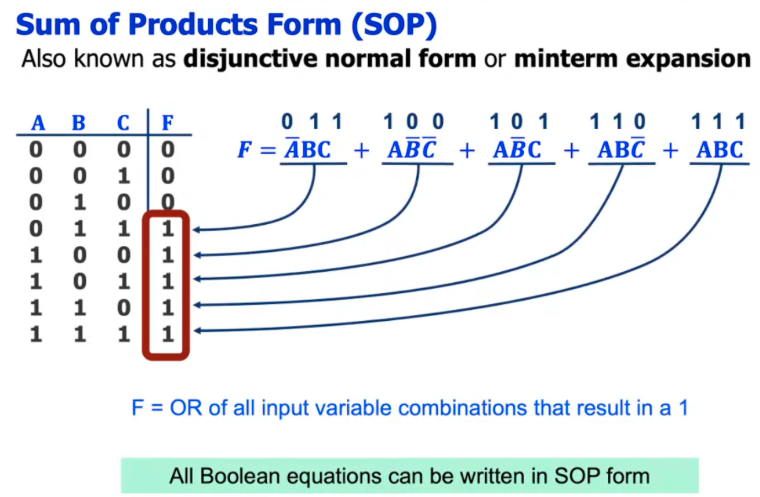
- Minterm: A product term (AND term) that includes all input variables, either in their true or complemented form. A minterm is 1 for exactly one row of the truth table.
- Maxterm: A sum term (OR term) that includes all input variables, either in their true or complemented form. A maxterm is 0 for exactly one row of the truth table.
Sum of Products (SOP) Form
The Sum of Products (SOP) form expresses a Boolean function as a sum (OR) of minterms. Each minterm corresponds to a row in the truth table where the function output is 1.
Steps:
- Identify Minterms: For each row in the truth table where the output is 1, create a minterm by ANDing together the literals corresponding to that row. If an input variable is 0 in that row, use its complement; if it’s 1, use the variable itself.
- Sum the Minterms: OR together all the minterms identified in step 1.
Example: