00 Anhänge Elektrotechnik Buch

Anhang A: Vektoren

Dieser Anhang behandelt die Grundlagen der Vektorrechnung.

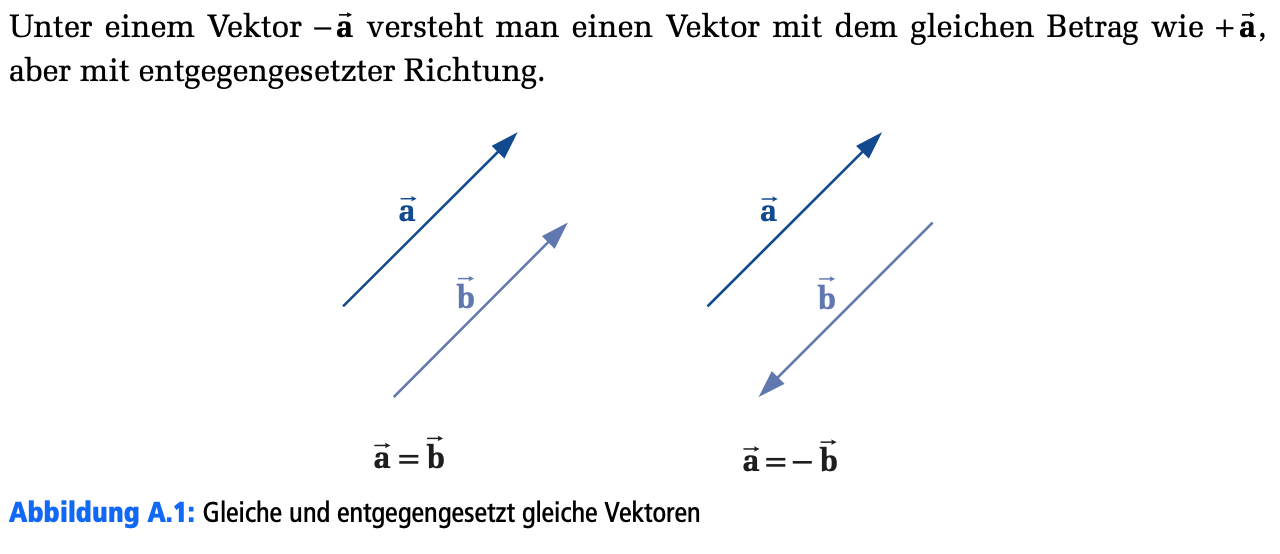
A.1 Einheitsvektoren

• Ein Einheitsvektor ${\vec{e}}_a$ hat den Betrag 1 ($|{\vec{e}}_a|=1$) und zeigt in eine bestimmte Richtung.
• Jeder Vektor $\vec{a}$ kann als Produkt seines Betrags $a=|\vec{a}|$ und eines Einheitsvektors in seiner Richtung dargestellt werden: $\vec{a}=a{\vec{e}}_a$.

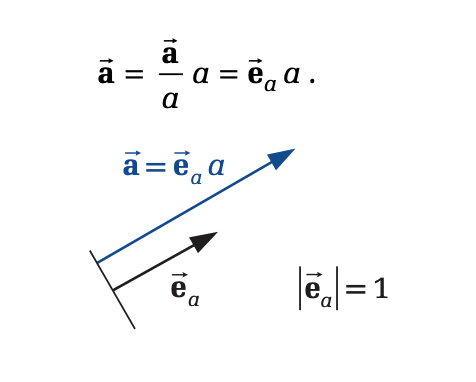
A.2 Einfache Rechenoperationen

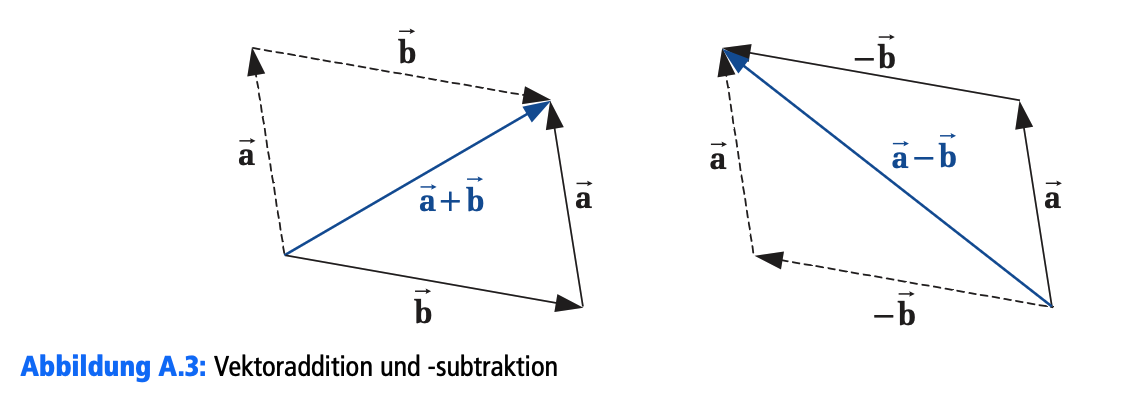
• Addition/Subtraktion: Vektoren werden komponentenweise addiert/subtrahiert oder grafisch aneinandergelegt. $\vec{a}\pm \vec{b}$.
• Multiplikation mit Skalar: Ein Vektor $\vec{a}$ multipliziert mit einem Skalar $p$ ergibt $p\vec{a}$, was die Länge des Vektors um den Faktor $|p|$ ändert und ggf. die Richtung umkehrt (wenn $p<0$).

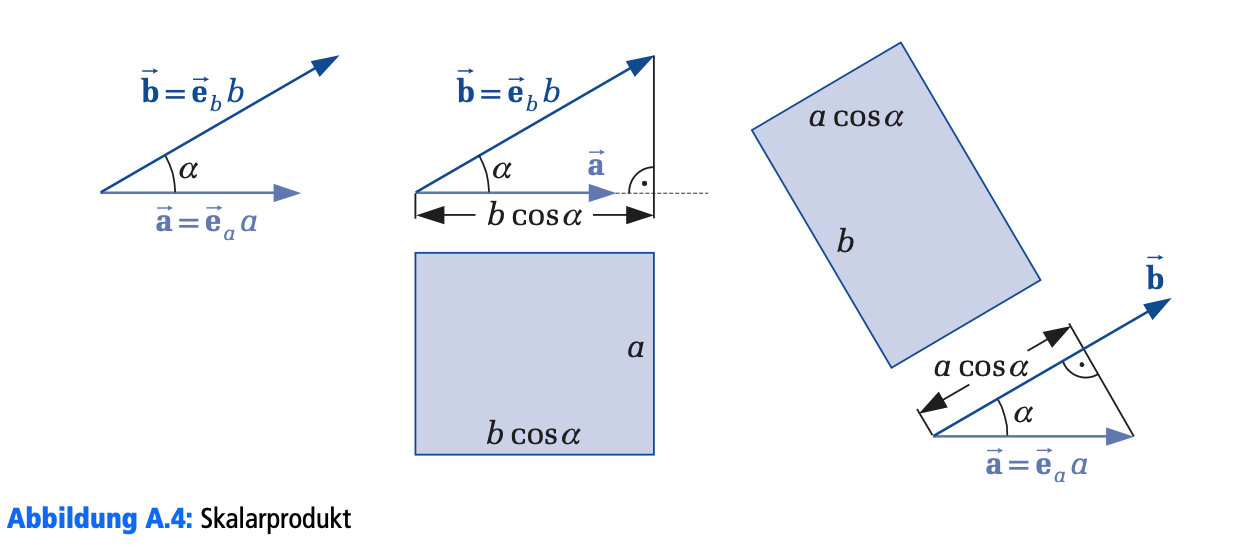
A.3 Das Skalarprodukt (Dot Product)

• Das Skalarprodukt zweier Vektoren $\vec{a}$ und $\vec{b}$ ist ein Skalar:

$\vec{a}\cdot \vec{b}\stackrel{\text{(A.2)}}{=}a{\vec{e}}_a\cdot b{\vec{e}}_b=ab{\vec{e}}_a\cdot {\vec{e}}_b=ab\cos \alpha$ $\vec{a}\cdot \vec{b}=ab\cos \alpha$ wobei $\alpha$ der Winkel zwischen den Vektoren ist.

• Es ist kommutativ: $\vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{a}$.
• Stehen Vektoren senkrecht aufeinander, ist ihr Skalarprodukt Null ($\vec{a}\cdot \vec{b}=0$, wenn $\alpha =90^{\circ }$).
• Sind Vektoren parallel, ist $\vec{a}\cdot \vec{b}=ab$. Sind sie antiparallel, ist $\vec{a}\cdot \vec{b}=-ab$.

Was sagt uns das Ergebnis? (Die Idee dahinter)

Das Skalarprodukt misst im Grunde, “wie sehr ein Vektor in die Richtung des anderen Vektors zeigt”.

Man kann es sich als Projektion vorstellen:

• Stell dir vor, du hast zwei Pfeile a und b, die an derselben Stelle starten.

• Du lässt eine “Sonne” senkrecht auf den Vektor b scheinen.

• Der Vektor a wirft einen Schatten auf die Linie, auf der b liegt.

• Das Skalarprodukt ist die Länge dieses Schattens (das ist $a\cos \alpha$) multipliziert mit der gesamten Länge von b.

A.4 Das Vektorprodukt (Cross Product)

• Das Vektorprodukt zweier Vektoren $\vec{a}$ und $\vec{b}$ ist ein Vektor $\vec{c}$: $\vec{c}=\vec{a}\times \vec{b}$
• Der Betrag ist $|\vec{c}|=ab\sin \alpha$, was der Fläche des von $\vec{a}$ und $\vec{b}$ aufgespannten Parallelogramms entspricht.
• Der Vektor $\vec{c}$ steht senkrecht auf der Ebene, die von $\vec{a}$ und $\vec{b}$ aufgespannt wird.
• Die Richtung von $\vec{c}$ folgt der Rechten-Hand-Regel ($\vec{a},\vec{b},\vec{c}$ bilden ein Rechtssystem).
• Es ist anti-kommutativ: $\vec{a}\times \vec{b}=-(\vec{b}\times \vec{a})$.
• Sind Vektoren parallel oder antiparallel, ist ihr Vektorprodukt der Nullvektor ($\vec{a}\times \vec{b}=\vec{0}$, wenn $\alpha =0^{\circ }$ oder $\alpha =180^{\circ }$).

A.5 & A.6 Vektorkomponenten & Vektorbeziehungen

• Ein Vektor $\vec{a}$ kann in orthogonale Komponenten zerlegt werden: $\vec{a}=a_x{\vec{e}}_x+a_y{\vec{e}}_y+a_z{\vec{e}}_z$ wobei $a_x=\vec{a}\cdot {\vec{e}}_x$, $a_y=\vec{a}\cdot {\vec{e}}_y$, $a_z=\vec{a}\cdot {\vec{e}}_z$.
• Betrag: $|\vec{a}|=a=\sqrt{a_x^2+a_y^2+a_z^2}$.
• Skalarprodukt: $\vec{a}\cdot \vec{b}=a_x{b}_x+a_y{b}_y+a_z{b}_z$.
• Vektorprodukt: $\vec{a}\times \vec{b}=(a_y{b}_z-a_z{b}_y){\vec{e}}_x+(a_z{b}_x-a_x{b}_z){\vec{e}}_y+(a_x{b}_y-a_y{b}_x){\vec{e}}_z$

A.7 Formeln zur Vektorrechnung

• Dieser Abschnitt listet wichtige Identitäten wie Distributivgesetze und Formeln für mehrfache Produkte (z.B. Spatprodukt $\vec{a}\cdot (\vec{b}\times \vec{c})$, BAC-CAB-Regel $\vec{a}\times (\vec{b}\times \vec{c})$).

---

Anhang B: Orthogonale Koordinatensysteme

Dieser Anhang beschreibt drei wichtige orthogonale Koordinatensysteme. Orthogonal bedeutet, dass die Einheitsvektoren an jedem Punkt senkrecht aufeinander stehen. Es handelt sich um Rechtssysteme.

B.1 Kartesisches Koordinatensystem $(x,y,z)$

• Koordinaten: $x,y,z$.
• Einheitsvektoren: ${\vec{e}}_x,{\vec{e}}_y,{\vec{e}}_z$ (konstant im Raum).
• Ortsvektor: $\vec{r}=x{\vec{e}}_x+y{\vec{e}}_y+z{\vec{e}}_z$.
• Vektorielles Wegelement: $d\vec{r}=dx{\vec{e}}_x+dy{\vec{e}}_y+dz{\vec{e}}_z$.
• Betrag des Wegelements: $(dr{)}^2=(dx{)}^2+(dy{)}^2+(dz{)}^2$.
• Volumenelement: $dV=dxdydz$.

B.2 Krummlinige orthogonale Koordinatensysteme $(u_1,u_2,u_3)$

• Allgemeine Beschreibung von Systemen, bei denen Koordinatenlinien gekrümmt sein können.
• Einheitsvektoren: ${\vec{e}}_1,{\vec{e}}_2,{\vec{e}}_3$ (i.A. ortsabhängig).
• Metrische Faktoren: $h_1,h_2,h_3$, die beschreiben, wie sich eine infinitesimale Änderung einer Koordinate $d{u}_i$ in eine tatsächliche Länge $d{l}_i=h_{i}d{u}_i$ übersetzt. $h_i=\left|\frac{\partial \vec{r}}{\partial u_i}\right|$
• Vektorielles Wegelement: $d\vec{r}=h_{1}d{u}_1{\vec{e}}_1+h_{2}d{u}_2{\vec{e}}_2+h_{3}d{u}_3{\vec{e}}_3$.
• Betrag des Wegelements: $(dr{)}^2=(h_{1}d{u}_1{)}^2+(h_{2}d{u}_2{)}^2+(h_{3}d{u}_3{)}^2$.
• Volumenelement: $dV=h_1{h}_2{h}_{3}d{u}_{1}d{u}_{2}d{u}_3$.

B.3 Zylinderkoordinaten $(\rho ,\varphi ,z)$

• Koordinaten: $\rho$ (Abstand zur z-Achse), $\varphi$ (Winkel zur x-Achse in xy-Ebene), $z$ (Höhe).
• Beziehung zu kartesisch: $x=\rho \cos \varphi$, $y=\rho \sin \varphi$, $z=z$.
• Einheitsvektoren: ${\vec{e}}_{\rho },{\vec{e}}_{\varphi },{\vec{e}}_z$ ( ${\vec{e}}_{\rho },{\vec{e}}_{\varphi }$ sind ortsabhängig).
• Metrische Faktoren: $h_{\rho }=1$, $h_{\varphi }=\rho$, $h_z=1$.
• Vektorielles Wegelement: $d\vec{r}=d\rho {\vec{e}}_{\rho }+\rho d\varphi {\vec{e}}_{\varphi }+dz{\vec{e}}_z$.
• Volumenelement: $dV=\rho d\rho d\varphi dz$.

B.4 Kugelkoordinaten $(r,\vartheta ,\varphi )$

• Koordinaten: $r$ (Abstand zum Ursprung), $\vartheta$ (Winkel zur z-Achse), $\varphi$ (Winkel zur x-Achse in xy-Ebene).
• Beziehung zu kartesisch: $x=r\sin \vartheta \cos \varphi$, $y=r\sin \vartheta \sin \varphi$, $z=r\cos \vartheta$.
• Einheitsvektoren: ${\vec{e}}_r,{\vec{e}}_{\vartheta },{\vec{e}}_{\varphi }$ (alle ortsabhängig).
• Metrische Faktoren: $h_r=1$, $h_{\vartheta }=r$, $h_{\varphi }=r\sin \vartheta$.
• Vektorielles Wegelement: $d\vec{r}=dr{\vec{e}}_r+rd\vartheta {\vec{e}}_{\vartheta }+r\sin \vartheta d\varphi {\vec{e}}_{\varphi }$.
• Volumenelement: $dV=r^2\sin \vartheta drd\vartheta d\varphi$.

(Hinweis: Der separate Abschnitt “Koordinatensysteme” auf S. 676 listet nur die Symbole für die in Anhang B erklärten Systeme auf.)

---

Anhang C: Ergänzungen zur Integralrechnung ∫

Erklärt zwei wichtige Integralarten für Vektorfelder.

C.1 Linienintegral einer vektoriellen Größe

• Berechnet das Integral eines Vektorfeldes $\vec{E}$ entlang einer Kurve $C$ von Punkt $P_A$ nach $P_B$. $W={\int }_{P_A}^{P_B}\vec{E}\cdot d\vec{s}$ $d\vec{s}$ ist das vektorielle Wegelement entlang der Kurve.
• Physikalische Bedeutung: z.B. die Arbeit $W$, die verrichtet wird, wenn eine Kraft $\vec{F}$ entlang eines Weges wirkt ($W=\int \vec{F}\cdot d\vec{s}$). In der Elektrotechnik oft zur Berechnung von Spannung ($U=\int \vec{E}\cdot d\vec{s}$).
• Ist das Integral über jeden geschlossenen Weg Null (${\oint }_C\vec{E}\cdot d\vec{s}=0$), nennt man das Feld ein konservatives Feld oder Potentialfeld (wie das elektrostatische Feld).

C.2 Fluss eines Vektorfeldes

• Berechnet den “Durchfluss” eines Vektorfeldes $\vec{D}$ durch eine Fläche $A$. $\Psi ={\iint }_A\vec{D}\cdot d\vec{A}$ $d\vec{A}=\vec{n}dA$ ist das vektorielle Flächenelement, wobei $\vec{n}$ der Normalenvektor zur Fläche ist.
• Physikalische Bedeutung: z.B. der Volumenstrom einer Flüssigkeit durch eine Fläche, oder der elektrische Fluss ${\Psi }_e$ bzw. magnetische Fluss ${\Psi }_m$.
• Ist das Integral über jede geschlossene Fläche $A$ Null (${\oint }_A\vec{D}\cdot d\vec{A}=0$), nennt man das Feld quellenfrei (wie das magnetische Feld). Ist es ungleich Null, entspricht es der eingeschlossenen Quellstärke (wie Ladung beim elektrischen Feld, Gauß’scher Satz).

---

Anhang D: Physikalische Grundbegriffe

Diskutiert die korrekte Handhabung physikalischer Größen und Gleichungen.

D.1 Physikalische Größen

• Eine physikalische Größe besteht aus einem Zahlenwert und einer Einheit (z.B. $l=18.3\text{m}$).
• SI-Basiseinheiten: Meter (m), Kilogramm (kg), Sekunde (s), Ampere (A), Kelvin (K), Mol (mol), Candela (cd).
• Abgeleitete Einheiten: Werden aus Basiseinheiten gebildet (z.B. Newton $N=\text{kg}\cdot \text{m}/{\text{s}}^2$).
• Dimension: Gibt den Zusammenhang mit Basisgrößen an (z.B. $\text{dim}(v)=\text{m}/\text{s}$).
• Vorsätze: Werden zur Skalierung verwendet (kilo, milli, mega, micro etc.).

D.2 Physikalische Gleichungen

• Größengleichungen: Gelten unabhängig von den gewählten Einheiten (z.B. $F=ma$). Einheiten werden wie algebraische Größen behandelt.
• Zugeschnittene Größengleichungen: Sind für spezifische Einheiten formuliert, oft um praktische Berechnungen zu vereinfachen. Das Ergebnis wird direkt in einer bestimmten Einheit erhalten, wenn die Eingangsgrößen in festgelegten Einheiten eingesetzt werden (z.B. Widerstandsberechnung S. 626). Vorsicht ist bei der Verwendung in anderen Kontexten geboten.

---

Anhang E: Komplexe Zahlen ℂ

Zusammenfassung der komplexen Zahlen und Rechenoperationen, wichtig für die Wechselstromrechnung.

E.1 Bezeichnungen

• Definition: $z=x+jy$, mit Realteil $x=\text{Re}\{z\}$ und Imaginärteil $y=\text{Im}\{z\}$. Die imaginäre Einheit ist $j=\sqrt{-1}$ ($j^2=-1$).
• Darstellungsformen:
  • Algebraisch (Kartesisch): $z=x+jy$
  • Trigonometrisch: $z=r(\cos \varphi +j\sin \varphi )$
  • Exponentiell (Polar): $z=r{e}^{j\varphi }$
• Betrag (Modul): $r=|z|=\sqrt{x^2+y^2}$.
• Argument (Phase, Winkel): $\varphi =\arg \{z\}=\arctan (y/x)$ (Achtung auf Quadranten!).
• Euler’sche Formel: $e^{j\varphi }=\cos \varphi +j\sin \varphi$.
• Konjugiert Komplexe Zahl: $z^{\ast }=x-jy=r{e}^{-j\varphi }$.

E.2 Rechenoperationen

• Addition/Subtraktion: Komponentenweise in algebraischer Form: $z_1\pm z_2=(x_1\pm x_2)+j(y_1\pm y_2)$.
• Multiplikation:
  • Algebraisch: $(x_1+j{y}_1)(x_2+j{y}_2)=(x_1{x}_2-y_1{y}_2)+j(x_1{y}_2+x_2{y}_1)$.
  • Exponentiell: $z_1{z}_2=r_1{r}_2{e}^{j({\varphi }_1+{\varphi }_2)}$ (Beträge multiplizieren, Winkel addieren).
• Division:
  • Algebraisch: Bruch mit $z_2^{\ast }$ erweitern.
  • Exponentiell: $z_1/z_2=(r_1/r_2)e^{j({\varphi }_1-{\varphi }_2)}$ (Beträge dividieren, Winkel subtrahieren).
• Multiplikation mit j: Drehung um $+90^{\circ }$ ($+\pi /2$) in der komplexen Ebene.
• Division durch j: Drehung um $-90^{\circ }$ ($-\pi /2$) in der komplexen Ebene.
• Potenzieren (Moivre): $z^n=(r{e}^{j\varphi }{)}^n=r^n{e}^{jn\varphi }=r^n(\cos (n\varphi )+j\sin (n\varphi ))$.
• Wurzelziehen: Die n-te Wurzel aus $z$ hat $n$ Lösungen: $z_k=\sqrt[n]{r}{e}^{j(\varphi +2k\pi )/n}\text{fu¨r }k=0,1,...,n-1$

---

Anhang F: Ergänzungen zu den Ortskurven

Liefert die mathematischen Beweise für die geometrischen Regeln der Inversion (Kehrwertbildung $w=1/z$) von Ortskurven in der komplexen Ebene.

• Inversion einer Geraden durch den Nullpunkt: Ergibt wieder eine Gerade durch den Nullpunkt (gespiegelt an der reellen Achse).
• Inversion einer Geraden, die nicht durch den Nullpunkt verläuft: Ergibt einen Kreis, der durch den Nullpunkt geht.
• Inversion eines Kreises, der durch den Nullpunkt geht: Ergibt eine Gerade, die nicht durch den Nullpunkt geht.
• Inversion eines Kreises, der nicht durch den Nullpunkt geht: Ergibt wieder einen Kreis (nicht durch den Nullpunkt).

---

Anhang G: Ergänzungen zur Fourier-Entwicklung

Vertieft Aspekte der Konvergenz von Fourier-Reihen.

G.1 Konvergenz der Fourier-Reihen

• Dirichlet-Bedingungen: Eine periodische Funktion kann in eine Fourier-Reihe entwickelt werden, wenn sie stückweise stetig ist und nur endlich viele Extrema pro Periode hat (in der Praxis meist erfüllt).
• Konvergenz:
  • An Stetigkeitsstellen konvergiert die Reihe gegen den Funktionswert $u(t)$.
  • An Sprungstellen $t_0$ konvergiert die Reihe gegen den Mittelwert des links- und rechtsseitigen Grenzwertes: $\frac{1}{2}[u(t_0+0)+u(t_0-0)]$.
• Konvergenz im Mittel: Der mittlere quadratische Fehler zwischen Funktion und Partialsumme geht gegen Null.
• Parseval’sche Gleichung: Stellt eine Energieerhaltung im Zeit- und Frequenzbereich dar. Das Integral des Betragsquadrats der Funktion über eine Periode ist proportional zur Summe der Betragsquadrate der Fourier-Koeffizienten. $\frac{1}{T}{\int }_0^T|u(t){|}^{2}dt=a_0^2+\frac{1}{2}{\sum }_{n=1}^{\infty }({\hat{a}}_n^2+{\hat{b}}_n^2)={\sum }_{n=-\infty }^{\infty }|{\hat{c}}_n{|}^2$
• Konvergenzgeschwindigkeit: Je “glatter” die Funktion (d.h. je mehr stetige Ableitungen sie besitzt), desto schneller fallen die Amplituden der höheren Harmonischen ab (z.B. wie $1/n^{k+1}$, wenn die k-te Ableitung die erste unstetige ist).

G.2 Gibbs’sches Phänomen

• In der Nähe von Sprungstellen schwingt die Partialsumme der Fourier-Reihe über den eigentlichen Funktionswert hinaus (“Overshoot”).
• Die Höhe des Überschwingens beträgt ca. 9% der Sprunghöhe auf jeder Seite, unabhängig von der Anzahl $N$ der berücksichtigten Terme.
• Mit steigendem $N$ wird der Bereich des Überschwingens schmaler und rückt näher an die Sprungstelle heran, aber die Höhe bleibt konstant.

---

Anhang H: Kleine mathematische Formelsammlung

Dieser Anhang listet nützliche Formeln und Tabellen auf.

• H.1 Additionstheoreme: Trigonometrische Identitäten (z.B. $\sin (x\pm y)$, $\cos (x\pm y)$, ${\sin }^{2}x$, ${\cos }^{2}x$, Summen zu Produkten etc.).
• H.2 Integrale: Stammfunktionen und bestimmte Integrale häufig vorkommender Funktionen, insbesondere trigonometrischer Produkte, die für die Fourier-Analyse relevant sind (Orthogonalitätsrelationen).
• H.3 Matrizen: Grundlegende Definitionen und Rechenregeln für Matrizen (Addition, Multiplikation, Inverse, Determinante einer 2x2-Matrix).
• H.4 Fourier-Entwicklungen: Tabelle mit Fourier-Reihen (Koeffizienten ${\hat{a}}_n,{\hat{b}}_n$ und Effektivwerte $U_{eff}$) für verschiedene Standard-Signalformen (Rechteck, Dreieck, Sägezahn, gleichgerichtete Sinus etc.).
• H.5 Tabellen zur Laplace-Transformation: Umfangreiche Tabelle mit Korrespondenzen zwischen Zeitfunktionen $u(t)$ (Originalbereich) und ihren Laplace-Transformierten $U(s)$ (Bildbereich).

---